Question

A survey showed that 84​% of adults need correction​ (eyeglasses, contacts,​ surgery, etc.) for their eyesight. If 22 adults are randomly​ selected, find the probability that no more than 1 of them need correction for their eyesight. Is 1 a significantly low number of adults requiring eyesight​ correction?

Answer 1

Answer with explanation:

The binomial distribution formula :-

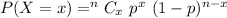`P(X=x)=^nC_x\ p^x\ (1-p)^(n-x)`, where P(x) is the probability of getting success in x trials , n is total number of trials and p is the probability of getting success in each trial.

Given : The probability that adults need correction for their eyesight = 0.84

If 22 adults are randomly​ selected, then the probability that no more than 1 of them need correction for their eyesight .

`P(X\leq1)=P(0)+P(1)\\\\=^(22)C_0\ (0.84)^(0)\ (1-0.84)^(22-0)+^(22)C_1\ (0.84)^1\ (1-0.84)^(22-1)\\\\=(0.84)^(0)(0.16)^(22)+22(0.84)(0.16)^(21)=3.6*10^(-16)`

which is much lower than 0.5 .

Yes , 1 is significantly low number of adults requiring eyesight​ correction .