Question

A wall with a surface area of 10 m2 is 2.5 cm thick. The inner surface temperature of the wall is 4150C, but the outer surface is much cooler. The heat loss through the wall is 3 kW, and the thermal conductivity is 0.2 W/m-K. a. What is the temperature of the outer surface of the wall? List all applicable assumptio

Answer 1

650.65 K or 377.5°C

Step-by-step explanation:

Area = A = 10 m²

Thickness of wall = L = 2.5 cm = 2.5×10⁻² m

Inner surface temperature of wall =
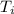`T_i` = 415°C = 688.15 K

Outer surface temperature of wall =
`T_o`

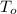
Heat loss through the wall = 3 kW = 3×10³ W

Thermal conductivity of wall = k = 0.2 W/m K

Assumptions made here as follows

1. There is not heat generation in the wall itself
2. The heat conduction is one dimensional
3. Heat flow follows steady state
4. The material has same properties in all directions i.e., it is homogeneous.

Considering the above assumptions we use the following formula

`Q=\frac {T_i-T_o}{(L)/(kA)}\\\Rightarrow T_o=T_i-\frac {QL}{kA}\\\Rightarrow T_o=688.15-\frac {3* 10^(3)* 2.5* 10^(-2)}{0.2* 10}\\\Rightarrow T_o=650.65~K`

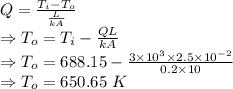
∴ The temperature of the outer surface of the wall is 650.65 K or 377.5°C