Given:
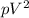 = constant (1)
= constant (1)
⇒
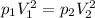 (2)
(2)


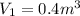
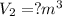
Solution:
Here, from eqn (1), the polytropic constant is '2' ( Since, here
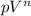 =
=
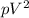 )
)
Now, using eqn (2), we get
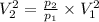
putting the values in above eqn, we get-
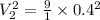
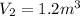
Now, work for the process is given by:
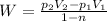 (3)
(3)
where,
n = potropic constant = 2
Using Eqn (3), we get:
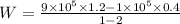
W = - 240 kJ