Answer:
The maximum value of C is 15
Explanation:
we have
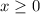 -----> constraint A
-----> constraint A
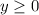 -----> constraint B
-----> constraint B
 -----> constraint C
-----> constraint C
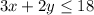 -----> constraint D
-----> constraint D
using a graphing tool
The solution area of the constraints in the attached figure
we have the vertices
(0,0),(0,9),(2,6),(5,0)
Substitute the value of x and the value of y in the objective function
(0,0) ----->

(0,9) ----->
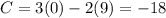
(2,6) ----->
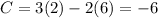
(5,0) ----->
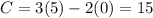
therefore
The maximum value of C is 15