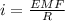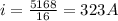Question

A strong electromagnet produces a uniform magnetic field of 1.60 T over a cross-sectional area of 0.340 m2. A coil having 190 turns and a total resistance of 16.0 Ω is placed around the electromagnet. The current in the electromagnet is then smoothly reduced until it reaches zero in 20.0 ms. What is the current induced in the coil?

Answer 1

i = 323 A

Step-by-step explanation:

Initial flux due to magnetic field from the coil is given as

`\phi = NB.A`

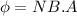
here we will have

`N = 190`

`B = 1.60 T`

`A = 0.340 m^2`

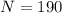
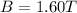
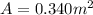
now the flux is given as

`\phi_1 = (190)(1.60)(0.340) = 103.36 T m^2`

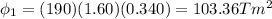
finally current in the electromagnet changed to zero

so final flux in the coil is zero

`\phi_2 = 0`

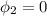
now we know that rate of change in flux will induce EMF in the coil

so we will have

`EMF = (\phi_1 - \phi_2)/(\Delta t)`

`EMF = (103.36 - 0)/(20 * 10^(-3))`

`EMF = 5168 Volts`

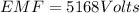
now induced current is given as

`i = (EMF)/(R)`

`i = (5168)/(16) = 323 A`