Question

A retiree receives $5120 a year interest from $40,000 placed in two bonds, one paying 14% and the other 12%. How much is invested in each bond? 3)

Answer 1

To find out how much is invested in each bond, set up a system of equations and solve for the values of x and y.

Step-by-step explanation:

To find out how much is invested in each bond, we can set up a system of equations.

Let x be the amount invested in the bond paying 14% interest, and y be the amount invested in the bond paying 12% interest.

We know that the retiree receives $5120 in interest each year. So, we have the equation:

x(0.14) + y(0.12) = 5120

Since the total amount invested is $40,000, we can also write the equation:

x + y = 40000

We can now solve this system of equations using any method, such as substitution or elimination, to find the values of x and y.

Answer 2

Investment in first bond is $ 16,000

In second bond is $ 24,000

Step-by-step explanation:

Let x be the amount invested in first bond,

Since, the total invested amount = $ 40,000,

So, the total amount invested in second bond = ( 40,000 - x ) dollars,

Given,

In first bond,

Interest rate = 14%,

While in second bond,

Interest rate = 12%,

Thus, the total interest from both bonds in a year,

I = 14% of x + 12% of ( 40,000 - x )

`=(14x)/(100)+(12(40000-x))/(100)`

`=0.14x+0.12(40000-x)`

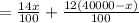
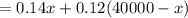
According to the question,

I = $ 5120,

`\implies 0.14x+0.12(40000-x)=5120`

`0.02x+4800=5120`

`0.02x=320`

`\implies x = 16000`

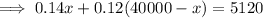
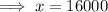
Hence, the amount invested in first bond = $ 16,000,

The amount invested in second bond = $ 40,000 - $ 16,000 = $ 24,000