Question

A reservoir delivers water to a horizontal pipeline 39 long The first 15 m has a diameter of 50 mm, after which it suddenly becomes 75 mm. The outlet of the reservoir is sharp. The flow rate is 2,8 l/s to atmosphere. Take f=0,0048 for the 50 mm pipe and f=0,0058 for the 75 pipe. Determine the difference between the vater level in the reservoir and the outlet of the pipe.

Answer 1

The difference of head in the level of reservoir is 0.23 m.

Step-by-step explanation:

For pipe 1

`d_1=50 mm,f_1=0.0048`

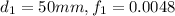
For pipe 2

`d_2=75 mm,f_2=0.0058`

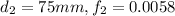
Q=2.8 l/s

`Q=2.8* 10^{-3]`

We know that Q=AV

`Q=A_1V_1=A_2V_2`

`A_1=1.95* 10^(-3)m^2`

`A_2=4.38* 10^(-3) m^2`

`So V_2=0.63 m/s,V_1=1.43 m/s`

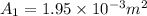
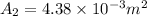
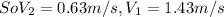
head loss (h)

`h=(f_1L_1V_1^2)/(2gd_1)+(f_2L_2V_2^2)/(2gd_2)+0.5(V_1^2)/(2g)`

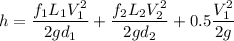
Now putting the all values

`h=(0.0048* 15* 1.43^2)/(2* 9.81* 0.05)+(0.0058* 24* 0.63^2)/(2* 9.81* 0.075)+0.5(1.43^2)/(2* 9.81)`

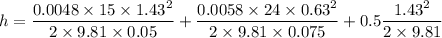
So h=0.23 m

So the difference of head in the level of reservoir is 0.23 m.