Answer:
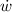 = -0.303 KW
= -0.303 KW
Step-by-step explanation:
This is the case of unsteady flow process because properties are changing with time.
From first law of thermodynamics for unsteady flow process
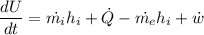
Given that tank is insulated so
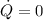 and no mass is leaving so
and no mass is leaving so
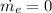
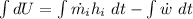
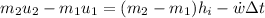
Mass conservation
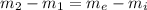
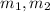 is the initial and final mass in the system respectively.
is the initial and final mass in the system respectively.
Initially tank is evacuated so
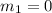
We know that for air
 ,
,

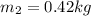
So now putting values
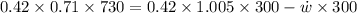
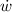 = -0.303 KW
= -0.303 KW