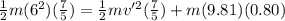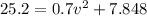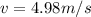Question

A solid ball with mass M and radius R is rolling (without slipping) on a flat surface at 6 m/s. It then gets to a small smooth hill and rolls up 80 cm to the top and continues rolling on a flat surface. (a) Explain why we are allowed to apply the conservation of energy to the ball although rolling requires friction. (b) Use conservation of energy to find the velocity of the ball after it has passed the hill. (Moment of inertia of a solid ball around its center of mass is 2 5 MR 2

Answer 1

Part B)

v = 4.98 m/s

Step-by-step explanation:

Part a)

As the ball is rolling on the inclined the the friction force will be static friction and the contact point of the ball with the plane is at instantaneous rest

The point of contact is not slipping on the ground so we can say that the friction force work done would be zero.

So here in this case of pure rolling we can use the energy conservation

Part b)

By energy conservation principle we know that

initial kinetic energy + initial potential energy = final kinetic energy + final potential energy

so we will have

`(1)/(2)mv^2 + (1)/(2)I\omega^2 = (1)/(2)mv'^2 + (1)/(2)I\omega'^2 + mgh`

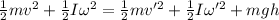
here in pure rolling we know that

`v = R\omega`

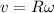
now from above equation we have

`(1)/(2)mv^2 + (1)/(2)((2)/(5)mR^2)((v)/(R))^2 = (1)/(2)mv'^2 + (1)/(2)((2)/(5)mR^2)((v')/(R))^2 + mgh`

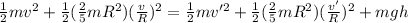
now we have

`(1)/(2)mv^2(1 + (2)/(5)) = (1)/(2)mv'^2(1 + (2)/(5)) + mgh`

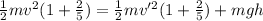
now plug in all values in it

`(1)/(2)m(6^2)((7)/(5)) = (1)/(2)mv'^2((7)/(5)) + m(9.81)(0.80)`

`25.2 = 0.7v^2 + 7.848`

`v = 4.98 m/s`