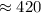Answer:a-396
b-420
Explanation:
 =0.1
=0.1
Margin of Error=0.04
Level of significance is z
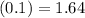
Previous estimate
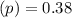
sample size is given by:
n=
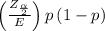
n=
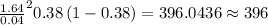
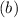 Does not use prior estimate
Does not use prior estimate
Assume
 =0.1
=0.1
Margin of Error=0.04
Level of significance is z
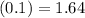
Population proportion
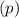 =0.5
=0.5
n=
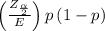
n=
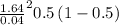
n=420.25