Given:
Outer Diameter, OD = 90 mm
thickness, t = 0.1656 mm
Poisson's ratio,
 = 0.334
= 0.334
Strength = 320 MPa
Pressure, P =3.5 MPa
Formula Used:
1).
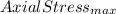 =
=
![P[(r_(o)^(2) + r_(i)^(2))/(r_(o)^(2) - r_(i)^(2))]](https://img.qammunity.org/2020/formulas/engineering/college/px5ix53816cjica9yeov97xwfw7ett7c0a.png)
2). factor of safety, m =
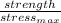
Step-by-step explanation:
Now, for Inner Diameter of cylinder, ID = OD - 2t
ID = 90 - 2(1.65) = 86.7 mm
Outer radius,
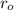 = 45mm
= 45mm
Inner radius,
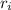 = 43.35 mm
= 43.35 mm
Now by using the given formula (1)
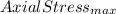 =
=
![3.5[(45^(2) + 43.35^(2))/(45^(2) - 43.35^(2))]](https://img.qammunity.org/2020/formulas/engineering/college/7lujzdm8h35pugobw5jplf8b6kl7162rcf.png)
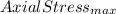 =
=
 =93.74 MPa
=93.74 MPa
Now, Using formula (2)
factor of safety, m = \frac{320}{93.74} = 3.414