Answer:
Explanation:
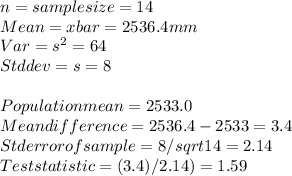
Since sample size is small and population std dev is not known, t test should be used.
p value = 0.135849
Since p>0.05 we accept that samples have a mean equal to 2533mm
There is no sufficient evidence to support the claim that the boards are either too long or too short