Question

A person 6 feet tall is walking away from a lamp post at the rate of 50 feet per minute. When the person is 4 feet from the lamp​ post, his shadow​ (see dashed​ line) is 10 feet long. Find the rate at which the length of the shadow is increasing when he is 12 feet from the lamp post.

Answer 1

125 feet per minute

Explanation:

Related rates are tricky enough, this one is especially tedious! This is a right triangle problem involving the concept of geometric means. The right triangle looks like this: It is one triangle with 2 heights, kind of like the pic I attached, but our larger triangle is right. But you can see that the heights are parallel to one another and that the "outside" height is longer than the "inside" height. Use that idea for this triangle. The smaller inside triangle has a height that is equal to the man's height, 6 ft, and his shadow is the base of the inside triangle, 10. The larger triangle has a height unknown (we need to find it) when the base of the larger triangle is 10 + 4 = 14. The geometric means can be used to find that longer height (which is also the height of the lamppost).

`(10)/(6)=(14)/(h)`

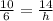
Cross multiply to solve for the height:

10h = 84 so

h = 8.4 ft

Now we have the longer height, its base, the shorter height (the height of the man, 6 ft), and that base of 10.

Letting x = length of shadow,

y = distance from person to lamppost, we need to find dx/dt when y = 12, given that dy/dy = 50.

Setting up the geometric means formula will give us the equation for which we need to find the implicit derivative with respect to time:

`(x)/(6) =(x+y)/(8.4)`

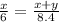
Cross multiply to get

8.4x = 6x + 6y. Since we are looking for dx/dt, we will solve that for x:

x = 2.5y

Now we take the derivative with respect to t:

`(dx)/(dt)=2.5(dy)/(dt)`

If dy/dt = 50, simply make the substitution:

`(dx)/(dt)=2.5(50)`

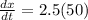
That gives us that the rate the shadow is changing is 125 feet per minute