Question

A particle is moving along a straight line with an initial velocity of 6 m/s when it is subjected to a deceleration of a- (-1.5v12) m/s2, where v is in m/s. Determine how far it travels before it stops. How much time does this take?

Answer 1

s= 6.53 m

t=3.27 s

Step-by-step explanation:

velocity = 6 m/s

deceleration = -1.5
`v^(1)/(2)`

`a=-1.5v^(1)/(2)\\v\frac{\mathrm{d} v}{\mathrm{d} s}=-1.5v^(1)/(2)\\-1.5ds=v^(1)/(2)dv\\\int\ {-1.5} \, ds= \int\ v^(1)/(2)dv\\-1.5s=(2)/(3)* v^{(3)/(2) }`

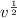
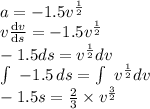
now inserting value of v=6s we get distance(s)

s= 6.53 m ( distance cannot be negative)

now for time calculation we know that

`a=\frac{\mathrm{d}v }{\mathrm{d} t}`

`-1.5v^(1)/(2) =\frac{\mathrm{d}v }{\mathrm{d} t}\\-1.5dt=(dv)/(v^(1)/(2)) \\\int -1.5 dt=\int v^{-(1)/(2)}dt \\1.5t=2v^(1)/(2)\\t=(4)/(3)v^(1)/(2)`

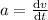
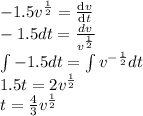
putting value of v=6s

t=3.27 s (time cannot be negative)