Question

A fluid with a relative density of 0.9 flows in a pipe which is 12 m long and lies at an angle of 60° to the horizontal At the top, the pipe has a diameter of 30 mm and a pressure gauge indicates a pressure of 860 kPa. At the bottom the diameter is 85 mm and a pressure gauge reading is 1 MPa. Assume the losses are negligible and determine the flov rate. Does the flow direction matter?

Answer 1

`Q=7.3* 10^(-3) m^3/s`

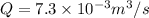
Step-by-step explanation:

Given that

At top
`d_2=30 mm,P_2=860 KPa ,P_1=1000 KPa,d_1=85 mm`

`\rho =900(Kg)/(m^3)`

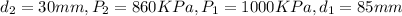
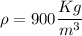
We know that

`(P_1)/(\rho g)+(V_1^2)/(2g)+Z_1=(P_2)/(\rho g)+(V_2^2)/(2g)+Z_2`

`A_1V_1=A_2V_2`

`(V_1)/(V_2)=\left((d_2)/(d_1)\right)^2`

`(V_1)/(V_2)=\left((30)/(85)\right)^2`

`V_2=8.02V_1`

`Z_2=12 sin60^(\circ)`

`(1000* 1000)/(900* 9.81)+(V_1^2)/(2* 9.81)+0=(860* 1000)/(900* 9.81 )+(V_2^2)/(2* 9.81)+12 sin60^(\circ)`

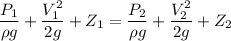
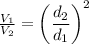
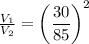
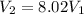
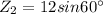
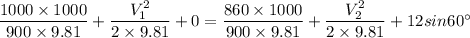
So
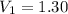`V_1=1.30`m/s

We know that flow rate Q=AV

`Q=A_1V_1`

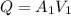
By putting the values

`A_1=(\pi)/(4)d^2`

`Q=7.3* 10^(-3) m^3/s`

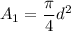
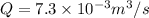
To find the flow rate we do not need the direction of flow,because we are just doing balancing of energy at inlet and at the exits of pipe.