Question

A flat rectangular door in a mine is submerged froa one side in vater. The door dimensions are 2 n high, 1 n vide and the vater level is 1,5 m higher than the top of the door. The door has two hinges on the vertical edge, 160 mm from each corner and a sliding bolt on the other side in the niddle. Calculate the forces on the hinges and sliding bolt. Hint: Consider the door from a side view and from a plaa vies respectively and take moments about a point each time.)

Answer 1

Force on the bolt = 24.525 kN

Force on the 1st hinge = 8.35 kN

Force on the 2nd hinge = 16.17 kN

Step-by-step explanation:

Given:

height = 2 m

width =1 m

depth of the door from the water surface = 1.5 m

Therefore,

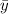`\bar{y}` =1.5+1 = 2.5 m

Hydrostatic force acting on the door is

`F= \rho * g* \bar{y}* A`

`F= 1000 * 9.81* 2.5* 2* 1`

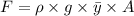
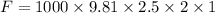
= 49050 N

= 49.05 kN

Now finding the Moment of inertia of the door about x axis

`I_(xx)=(1)/(12)* b* h^(3)`

`I_(xx)=(1)/(12)*1* 2^(3)`

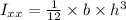
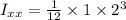
= 0.67

Now location of force,
`y^(*)`

`y^(*)=\bar{y}+\frac{I_(xx)}{A* \bar{y}}`

`y^(*)=2.5+(0.67)/(2* 1* 2.5)`

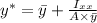
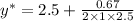
= 2.634

Therefore, calculating the unknown forces

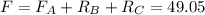`F=F_(A)+R_(B)+R_(C) = 49.05` ------------------(1)

Now since
`\sum M_{R_(A)}=0`

∴
`R_(B)* L+R_(C)* L-F* (1)/(2)=0`

`R_(B)+R_(C)-F* (1)/(2)=0`

`R_(B)+R_(C)=(F)/(2)`

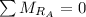
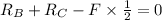
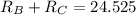`R_(B)+R_(C)=24.525` -----------------------(2)

From (1) and (2), we get

`R_(A) = 49.05-24.525`

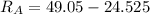
= 24.525 kN

This is the force on the Sliding bolt

Taking
`\sum M_{R_(C)}=0`

`F* 0.706-R_(A)* 0.84-R_(B)* 1.68 = 0`

`49.05* 0.706-24.525* 0.84-R_(B)* 1.68 = 0`

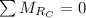
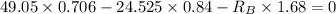
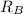`R_(B)` =8.35 kN

This is the reaction force on the 1st hinge.

Now from (1), we get

`R_(C)` =16.17 kN

This is the force on the 2nd hinge.