Question

A bit out of practice, but how to go about finding the origin and vertix of this equation

9x^(2)+16y^(2)=144

Answer 1

Answer:Explained Below

Explanation:

The given equation is similar to an ellipse which is in the form of

`(x^2)/(a^2)`+
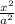`(y^2)/(b^2)`=1

where

2a=length of major axis

2b=length of minor axis

Here after rearranging the given equation we get

`(x^2)/((144)/(9))`+
`(y^2)/((144)/(16))`=1

`(x^2)/(16)`+
`(y^2)/(9)`=1

`(x^2)/(4^2)`+
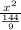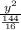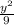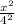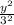`(y^2)/(3^2)`=1

therefore its origin is (0,0)

and vertices are
`\left ( \pm4,0\right )`&
`\left ( 0,\pm3\right )`

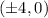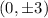
We can find origin by checking what is with x in the term
`\left ( x-something\right )^(2)`

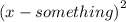
same goes for y

for
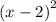`\left ( x-2\right )^(2)` here 2 is the x coordinate of ellipse

and for vertices Each endpoint of the major axis is vertices and each endpoint of minor axis is co-vertices