Question

A 100-mm-diametre shaft is subjected to a 10-kN.m steady bending moment, an 8-kN.m steady torque, and a 150-kN axial force. The yield strength of the shaft material is 600 MPa. Use the Tresca and the Von Mises theories to determine the safety factors for the given loadings.

Answer 1

Tresca FOS ,N=4.49

Von mises theory FOS N=4.27

Step-by-step explanation:

Cross sectional area of shaft A=
`(\pi )/(4)d^2`

`A=7.8* 10^(-3)`

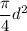
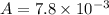
Bending stress
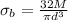`\sigma _b=(32M)/(\pi d^3)` =101.91 MPa (M=10 KN-m)

Shear stress
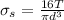`\sigma _s=(16T)/(\pi d^3)` =40.76 MPa (T=8 KN-m)

Axial stress
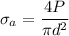`\sigma _a=(4P)/(\pi d^2)`=19.23 MPa

Now find the principle stress

`\sigma _1,\sigma_2=(\sigma_a+\sigma_b)/(2)\pm\sqrt {\left ((\sigma_a+\sigma_b)/(2)\right )^2+\tau ^2}`

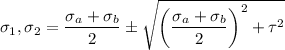
Now put the values

`\sigma _1,\sigma_2=(19.23+101.91)/(2)\pm\sqrt {\left ((19.23+101.91)/(2)\right )^2+40.76^2}`

`\sigma _1=133.62 ,\sigma _2= -12.42 MPa`

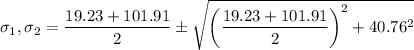
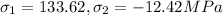
From tresca theory

`\tau _(max)=(\sigma _y)/(2N)`

`(\sigma _1-\sigma_2)/(2)=(600)/(2N)`

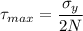
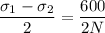
N=4.49

From Von mises theory

`\sigma _1^2+\sigma _2^2-\sigma _1\sigma _2=\left ((\sigma_y)/(N)\right )^2`

`133.62^2+\12.42^2+133.62* 12.42=\left((600)/(N)\right )^2`

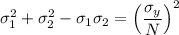
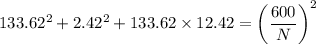
N=4.27