Question

A rectangle is inscribed with its base on the x-axis and its upper corners on the parabola y = 11 − x 2 . What are the dimensions of such a rectangle with the greatest possible area?

Answer 1

Answer:
`(22)/(3)`,
`2\dot \sqrt{(11)/(3)}`

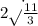
Explanation:

Given

rectangle with its base on x-axis

and other two corners at parabola

and parabola is downward facing symmetric about y-axis

let y be the y co-ordinate of the corner thus x co-ordinate is given by

`x=\pm √(11-y)`

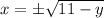
Thus lengths of rectangle is
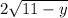`2√(11-y)` & y

Area
`=y* 2√(11-y)`

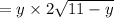
differentiating w.r.t to y for maximum area

`\frac{\mathrm{d} A}{\mathrm{d} y}=2* √(11-y)-(y)/(2\dot √(11-y))=0`

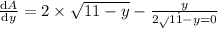
we get y=
`(22)/(3)`

and
`x=\pm \sqrt{(11)/(3)}`

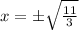
A_{max}=16.21 units