Question

A playground merry-go-round of radius R = 2.20 m has a moment of inertia I = 275 kg · m2 and is rotating at 9.0 rev/min about a frictionless vertical axle. Facing the axle, a 23.0-kg child hops onto the merry-go-round and manages to sit down on the edge. What is the new angular speed of the merry-go-round? rev/min

Answer 1

6.4 rpm

Step-by-step explanation:

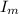`I_(m)` = moment of inertia of merry-go-round = 275 kgm²

m = mass of the child = 23 kg

R = radius of the merry-go-round = 2.20 m

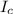`I_(c)` = moment of inertia of child after jumping on merry-go-round = mR² = (23) (2.20)² = 111.32 kgm²

Total moment of inertia after child jumps is given as

`I_(f)` =
`I_(m)` +
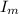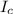`I_(c)` = 275 + 111.32 = 386.32 kgm²

Total moment of inertia before child jumps is given as

`I_(i)` =
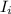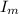`I_(m)` = 275 kgm²

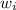`w_(i)` = initial angular speed = 9 rpm

`w_(f)` = final angular speed

using conservation of angular momentum

`I_(i)`
`w_(i)` =
`I_(f)`
`w_(f)`

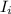
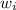(275) (9) = (386.32)
`w_(f)`

`w_(f)` = 6.4 rpm