Question

A flywheel made of Grade 30 cast iron (UTS = 217 MPa, UCS = 763 MPa, E = 100 GPa, density = 7100 Kg/m, Poisson's ratio = 0.26) has the following dimensions: ID = 150mm, OD = 250 mm and thickness = 37 mm. What is the rotational speed in rpm that would lead to the flywheel's fracture?

Answer 1

N = 38546.82 rpm

Step-by-step explanation:

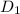`D_(1)` = 150 mm

`A_(1)= (\pi )/(4)* 150^(2)`

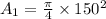
= 17671.45
`mm^(2)`

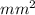
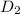`D_(2)` = 250 mm

`A_(2)= (\pi )/(4)* 250^(2)`

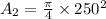
= 49087.78
`mm^(2)`

The centrifugal force acting on the flywheel is fiven by

F = M (
`R_(2)` -
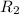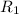`R_(1)` ) x
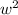`w^(2)` ------------(1)

Here F = ( -UTS x
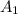`A_(1)` + UCS x
`A_(2)` )

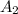Since density,
`\rho = (M)/(V)`

`\rho = (M)/(A* t)`

`M = \rho * A* t`
`M = 7100 * (\pi )/(4)\left ( D_(2)^(2)-D_(1)^(2) \right )* t`

`M = 7100 * (\pi )/(4)\left ( 250^(2)-150^(2) \right )* 37`

`M = 8252963901`

∴
`R_(2)` -
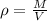
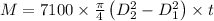
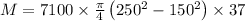
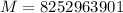
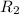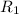`R_(1)` = 50 mm

∴ F =
`763* (\pi )/(4)* 250^(2)-217* (\pi )/(4)* 150^(2)`

F = 33618968.38 N --------(2)

Now comparing (1) and (2)

`33618968.38 = 8252963901* 50* \omega ^(2)`

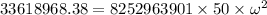
∴ ω = 4036.61

We know

`\omega = (2\pi N)/(60)`

`4036.61 = (2\pi N)/(60)`

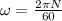
∴ N = 38546.82 rpm