Question

27-28 . Find the acute angles between the curves at their points of intersection. (The angle between two curves is the angle between their tangent lines at the point of intersection. 27. y = x, y = x 28. y = sinx, y = cos x, 0

Answer 1

27.The angle between two given curves is
`0^(\circ)`.

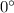28.
`\theta=tan^(-1)(2\sqrt2)`

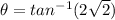
Explanation:

27.We are given that two curves

y=x,y=x

We have to find the angle between the two curves

The angle between two curves is the angle between their tangent lines at the point of intersection

We know that the values of both curves at the point of intersection are equal

Let two given curves intersect at point
`(x_1,y_1)`

Then
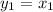`y_1=x_1` because both curves are same

`(dy)/(dx)=1`

`m_1=1,m_2=1`

`m_1(x_1)=1,m_2(x_1)=1`

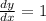
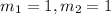
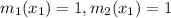
Using formula of angle between two curves

`tan\theta=(m_1(x_0)-m_2(x_0))/(1+m_1(x_0)m_2(x_0))`

`tan\theta=(1-1)/(1+1)=(0)/(2)=0`

`tan\theta=tan 0^(\circ)`

`\theta=0^(\circ)`

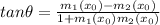
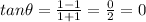
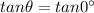
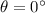
Hence,the angle between two given curves is
`0^(\circ)`.

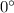28.y=sin x

y= cos x

By similar method we solve these two curves

Let two given curves intersect at point (x,y) then the values of both curves at the point are equal

Therefore, sin x = cos x

`(sin x)/(cos x)=1`

`tan x=1`

`tan x=(sin x)/(cos x)`

`tan x= tan (\pi)/(4)`

`x=(\pi)/(4)`

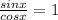
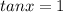
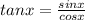
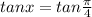
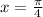
Now, substitute the value of x then we get y

`y= sin (\pi)/(4)=(1)/(\sqrt2)`

`sin (\pi)/(4)=cos (\pi)/(4)=(1)/(\sqrt2)`

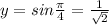
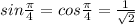
The values of both curves are same therefore, the point
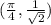`((\pi)/(4),(1)/(\sqrt2))` is the intersection point of two curves .

`m_1=cos x`

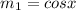
At
`x=(\pi)/(4)`

`m_1=(1)/(\sqrt2)`

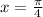
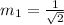
and

`m_2=-sin x=-(1)/(\sqrt2)`

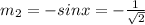
Substitute the values in the above given formula

Then we get
`tan\theta =((1)/(\sqrt2)+(1)/(\sqrt2))/(1-(1)/(2))`

`tan\theta=((2)/(\sqrt 2))/((1)/(2))`

`tan\theta=(2)/(\sqrt 2)* 2`

`tan\theta=(4)/(\sqrt2)=(4)/(\sqrt 2)*(\sqrt2)/(\sqrt2)`

`tan\theta=2\sqrt2`

`\theta=tan^(-1)(2\sqrt2)`

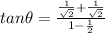
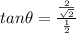
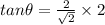
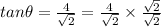
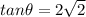
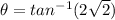
Hence, the angle between two curves is
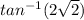`tan^(-1)(2\sqrt2)`.