Question

) A motor boat weighs 32,000 lb and its motor provides a force of 5000 lb. Assume that the water resistance is 100 pounds per foot per second of the velocity of the boat. Then 1000 dv dt = 5000 − 100v. If the boat starts from rest, what is the maximum velocity of the boat?

Answer 1

Maximum velocity, v = 50 ft/s

Explanation:

Given

1000
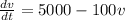`(dv)/(dt)=5000-100v` -----------(1)

Dividing (1) by 1000, we get

`(dv)/(dt)=5-(v)/(10)`

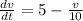
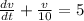`(dv)/(dt)+(v)/(10)=5` -----------------(2)

Now we can solve the above equation using method of integrating factors

`u(t)=e^{\int (1)/(10)dt}`

`u(t)=e^{(1)/(10)t}`

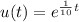
Now multiplying each side of (2) by integrating factor,

`e^{(1)/(10)t}((dv)/(dt))+(v)/(10)e^{(1)/(10)t}=5e^{(1)/(10)t}`

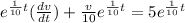
Combining the LHS into one differential we get,

`(d)/(dt)\left ( e^{(1)/(10)t}v \right ) = \int 5e^{(1)/(10)t}.dt`

`e^{(1)/(10)t}v = 50e^{(1)/(10)t}` + c

v(t)=50+ce

Appltying the initial condition v(0)=0, we get

`0=50+ce^{-(1)/(10)(0)}`

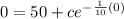
0=50+c

c=-50

So the particular solution is

`v(t)=50-50e^{-(1)/(10)t}`

`v(t)=50\left (1-e^{-(1)/(10)t}\right)`

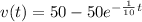
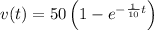
Therefore, the maximum velocity is 50 ft/s