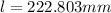Answer:
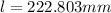
Step-by-step explanation:
Given:
Elastic modulus, E = 102 GPa
Diameter, d = 3.8mm = 0.0038 m
Applied tensile load = 2440N
Maximum allowable elongation, = 0.47mm = 0.00047
Now,
The cross-sectional area of the specimen,
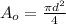
substituting the values in the above equation we get
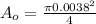
or
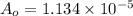
now
the stress (σ) is given as:

and
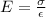
where,
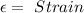
also,
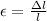
where,
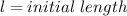
thus,
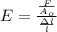
or on rearranging we get,
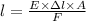
substituting the values in the above equation we get
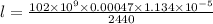
or
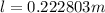
or