Question

A heap of rubbish in the shape of a cube is being compacted into a smaller cube. Given that the volume decreases at a rate of 3 cubic meters per minute, find the rate of change of an edge, in meters per minute, of the cube when the volume is exactly 8 cubic meters.

Answer 1

-1/4 meter per minute

Explanation:

Since, the volume of a cube,

`V=r^3`

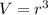
Where, r is the edge of the cube,

Differentiating with respect to t ( time )

`(dV)/(dt)=3r^2(dr)/(dt)`

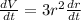
Given,
`(dV)/(dt)=-3\text{ cubic meters per minute}`

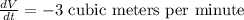
Also, V = 8 ⇒ r = ∛8 = 2,

By substituting the values,

`-3=3(2)^2 (dr)/(dt)`

`-3=12(dr)/(dt)`

`\implies (dr)/(dt)=-(3)/(12)=-(1)/(4)`

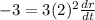
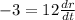
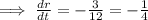
Hence, the rate of change of an edge is -1/4 meter per minute.