Question

A curve ball is a type of pitch in which the baseball spins on its axis as it heads for home plate. If a curve ball is thrown at 34.5 m/s (77 mph ) with a spin rate of 26 rev/s , how many revolutions does it complete before reaching home plate? Assume that home plate is 18.3 m (60 ft) from the pitching mound and that the baseball travels at a constant velocity.

Answer 1

The number of revolutions is 13.78

Step-by-step explanation:

Given data:

v = speed = 34.5 m/s

d = distance = 18.3 m

spin rate = 26 rev/s

The time taken is equal to:

`t=(d)/(v) =(18.3)/(34.5) =0.53s`

The number of revolutions is equal:

N = 0.53 * 26 = 13.78 rev

Answer 2

13.79 revolutions

Step-by-step explanation:

Velocity of ball = v = 34.5 m/s

Spin rate of ball = 26 revolutions/s

Distance between home plate and pitching mound = s = 18.3 m

Time taken by the ball to reach the home plate = t

`t=(18.3)/(34.5)\ s`

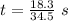
Number of revolutions the ball completes is

`26* (18.3)/(34.5)=13.79`

∴Number of revolutions the ball completes before reaching home plate is 13.79