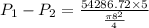Question

A closed cylindrical tank that is 8 ft in diameter and 24 ft long is completely filled with gasoline. The tank, with its long axis horizontal, is pulled by a truck along a horizontal surface. Determine the pressure difference between the ends (along the long axis of the tank) when the truck undergoes an acceleration of 5 ft/s2.

Answer 1

`P_(1)-P_(2)=5400lb/ft^(2)`

Step-by-step explanation:

We shall use newtons second law to evaluate the pressure difference

For the system the forces that act on it as shown in the figure

Thus by Newton's second law

`F_(1)-F_(2)=mass* acceleration\\\\P_(1)* Area-P_(2)* Area=mass* acceleration\\\\\because Force=Pressure* Area\\\\\therefore P_(1)-P_(2)=(mass* acceleration)/(Area)`

Mass of the gasoline can be calculated from it's density
`45lb/ft^(3)`

`Mass=Density* Volume\\\\Mass= 45lb/ft^(3)* \pi (d^(2))/(4)L\\\\Mass=45lb/ft^(3)*(\pi 8^(2))/(4)* 24\\Mass=54286.72lbs`

Using the calculated values we get

`P_(1)-P_(2)=(54286.72* 5)/((\pi 8^(2))/(4))`

`P_(1)-P_(2)=5400lb/ft^(2)`