Question

Discrete Math HELP!

let p ={Aaron, bob, phill, john, chad}

how many subsets contain neither Aaron nor bob

the answer is 2^(5-2)= 2^(3)= 8

but another question i saw was A = {1, 2, 3, 4, 5 ,6 ,7}

how many subsets of A INCLUDE {2, 4, 6}

and the anwser is 2^(7-3)= 2^4=16

why is the method we use for include and niether the same? I doubt there is an error becuase these questions were done by my professor.

Answer 1

Answer with Step-by-step explanation:

1.Let p={Aaron , bob ,phill,john,chad}

Number of elements in set p=5

Formula : Number of subset of the set which contain n elements

`2^n`

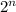
Total number of subset =
`2^5=32`

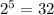
The subsets which contain neither Aaron nor bob are

{phil},{john},{chad}
`,\phi`,{phil,john},{phil,chad},{john,chad},{phil,john,chad}

There are eight subsets which do not contain neither Aaron nor bob .

Answer given by the method
`2^(5-2)=8`

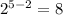
Where 5= Total number of elements

2= Number of elements in subsets which do not contain

Therefore,answer is correct.

2.A={1,2,3,4,5,6,7}

There are total seven elements

Therefore, total number of subsets =
`2^7`

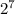
We have to find the number of subsets of A which include 2,4 and 6.

The number of subsets which contain {2,4, 6}

{2,4,6},{2,4,6,1},{2,4,6,3},{2,4,6,5},{2,4,6,7},{1,2,3,4,6},{1,2,4,5,6},{1,2,4,6,7},{2,4,5,6,7},{2,3,4,5,6},{2,3,4,6,7},{1,2,3,4,5,6},{2,3,4,5,6,7},{1,3,4,5,6,7},{1,2,4,5,6,7},{1,2,3,5,6,7},{1,2,3,4,5,7},{1,2,3,4,5,6,7}

Total number of subsets which contain {2,4,6} are eighteen.

Answer given by
`2^(7-3)=2^4=16`

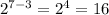
The answer is false.

We can not use these method for calculating number of subsets which contain{2,4,6}.