Question

A block of mass 0.221 kg is placed on top of a light, vertical spring of force constant 5365 N/m and pushed downward so that the spring is compressed by 0.097 m. After the block is released from rest, it travels upward and then leaves the spring. To what maximum height above the point of release does it rise?

Answer 1

The maximum height above the point of release is 11.653 m.

Step-by-step explanation:

Given that,

Mass of block = 0.221 kg

Spring constant k = 5365 N/m

Distance x = 0.097 m

We need to calculate the height

Using stored energy in spring

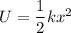`U=(1)/(2)kx^2`...(I)

Using gravitational potential energy

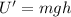`U' =mgh`....(II)

Using energy of conservation

`E_(i)=E_(f)`

`U_(i)+U'_(i)=U_(f)+U'_(f)`

`(1)/(2)kx^2+0=0+mgh`

`h=(kx^2)/(2mg)`

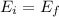
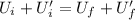
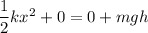
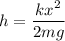
Where, k = spring constant

m = mass of the block

x = distance

g = acceleration due to gravity

Put the value in the equation

`h=(5365*(0.097)^2)/(2*0.221*9.8)`

`h=11.653\ m`

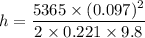
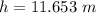
Hence, The maximum height above the point of release is 11.653 m.