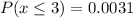Answer: 0.0031
Explanation:
Binomial distribution formula :-
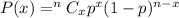 , where P(x) is the probability of x successes in the n independent trials of the experiment and p is the probability of success.
, where P(x) is the probability of x successes in the n independent trials of the experiment and p is the probability of success.
Given : A binomial probability experiment is conducted with the given parameters.
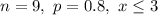
Now,
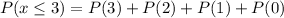
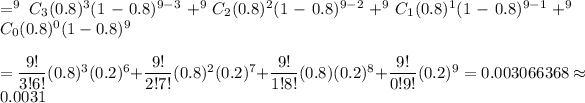
Hence,