Question

A baseball team plays in a stadium that holds 55,000 spectators. With ticket prices at $10, the average attendance had been 27,000. When ticket prices were lowered to $8, the average attendance rose to 33,000. (a) Find the demand function (price p as a function of attendance x), assuming it to be linear.

Answer 1

demand fuction: Q= 54,000 - 3,000p

Step-by-step explanation:

A linear function is represented as: y = a + bx

in this case: Q = a -bp

`\left[\begin{array}{ccc}x&y\\8&33,000\\10&27,000\end{array}\right]`

Using the line cross two point formula we got b:

`\left[\begin{array}{cc}x&y\\8&33,000\\10&27,000\end{array}\right]`

`b = (y_1 - y_2)/(x_2 - x_1) \\\\(33,000 - 27,000)/(8 - 10) \\6,000/(-2) = (-3,000)`

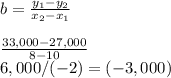
then we solve for a

33,000 = a -3000 x 8

33,000 = a - 24,000

54,000 = a

demand fuction: Q= 54,000 - 3,000p