Question

One solution of 21x^2 + bx -4 = 0 is -4/3. Find b and the other solution.​

Answer 1

see explanation

Explanation:

Given that x = -
`(4)/(3)` is a solution of the equation, then

Substitute this value into the equation and solve for b

21 (-
`(4)/(3)` )² + b (-
`(4)/(3)` ) - 4 = 0

21 ×
`(16)/(9)` -
`(4)/(3)` b - 4 = 0

`(112)/(3)` -
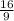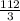`(4)/(3)` b - 4 = 0

Multiply through by 3

112 - 4b - 12 = 0

100 - 4b = 0 ( subtract 100 from both sides )

- 4b = - 100 ( divide both sides by - 4 )

b = 25 ← value of b

The equation can now be written as

21x² + 25x - 4 = 0 ← in standard form

with a = 21, b = 25, c = - 4

Use the quadratic formula to solve for x

x = ( - 25 ±
`√(25^2-(4(21)(-4))` ) / 42

= ( - 25 ±
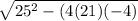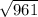`√(961)` ) / 42

= ( - 25 ± 31 ) / 42

x =
`(-25-31)/(42)` =
`(-56)/(42)` = -
`(4)/(3)`

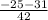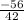or x =
`(-25+31)/(42)` =
`(6)/(42)` =
`(1)/(7)`

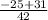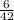The other solution is x =
`(1)/(7)`