Question

Find the point that splits segment AB in half if point A is located at (4,3) and point B is located at

(-2,6).​

Answer 1

(1, 4.5 )

Explanation:

The required point is at the midpoint of AB

Use the midpoint formula

Given A(4, 3) and B(- 2, 6 ), then

midpoint = [ 0.5(4 - 2), 0.5(3 + 6) ] = (1, 4.5 )

Answer 2

The point that splits the segment AB in half is
`C\left ( 1,4.5 \right )`

Explanation:

Given: Point A is located at
`\left ( 4,3 \right )` and point
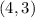`\left ( -2,6 \right )`

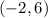
To find: Point that splits segment AB in half.

Solution: Let
`C\left ( x_(3),y_(3) \right)` be the point that splits AB in half.

We know that the mid point
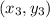`\left ( x_(3),y_(3) \right )` of a line segment joining the points
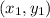`\left ( x_(1),y_(1) \right )` and
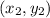`\left ( x_(2),y_(2) \right )` is calculated as
`\left ((x_(1)+x_(2))/(2),\:(y_(1)+y_(2))/(2) \right )`

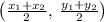
Here,
`x_(1)=4,\:x_(2)=-2,y_(1)=3,y_(2)=6`

`x_(3)=(4-2)/(2)`

`x_(3)=(2)/(2)`

`x_(3)=1`

`y_(3)=(3+6)/(2)`

`y_(3)=(9)/(2)`

`y_(3)=4.5`

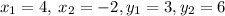
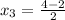
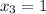
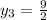
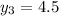
Hence, the point that splits the segment AB in half is
`C\left ( 1,4.5 \right )`