1 Answer

Michal J Figurski · Answer 1 · 2020-02-10T05:10:16+0000

Answer: 1.8°

Explanation:

To calculate the angle between the vectors u and v we use the formula of the dot product.

The dot product between two vecotores is:

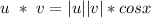
$u\ *\ v = |u||v|*cosx$

Where x is the angle between the vectors

As we know the components of both vectors, we calculate the dot product by multiplying the components of both vectors

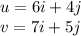
$u=6i + 4j\\v=7i +5j$

Then:

$u\ *\ v = 6*7 + 4*5$

$u\ *\ v = 42 + 20$

$u\ *\ v =62$

Now we calculate the magnitudes of both vectors

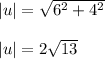
$|u|=√(6^2 + 4^2)\\\\|u|=2√(13)$

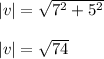
$|v|=√(7^2 +5^2)\\\\|v|=√(74)$

Then:

62 = 2√(13)*√(74)*cosx

Now we solve the equation for x

$62 = [tex]cosx=(62)/(2√(13)*√(74))\\\\x=arcos((62)/(2√(13)*√(74)))\\\\x=1.8\°$

Please log in or register to add a comment.