Answer: Option 'c' is correct.
Explanation:
Since we have given that
Perimeter of rectangular region = 144 feet
We need to find the maximum area .
As we know that the area will be maximum iff it is a square.
So, perimeter is given by
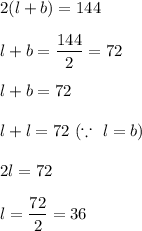
So, the maximum area would be
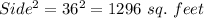
Hence, Option 'c' is correct.