Step-by-step explanation:
We know
the frequency of the tube with one end open and the other end closed follows the given relations as
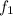 :
:
 :
:
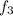 :
:
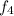 = 1 : 3 : 5 : 7
= 1 : 3 : 5 : 7
∴ the 4th allowed wave is
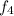 = 7
= 7
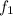
=
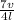
We know
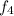 = 1975 Hz and v = 343 m/s ( as given in question )
= 1975 Hz and v = 343 m/s ( as given in question )
∴

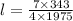
= 0.303 m
We know that v =
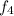 x
x
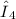
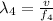
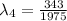
= 0.17 m
Now when the warmer air is flowing, the speed gets doubled and the mean temperature increases. And as a result the wavelength increases but the amplitude and the frequency remains the same.
So we can write
v ∝ λ
or

Therefore, the wavelength becomes doubled = 0.17 x 2
= 0.34 m
Now the new length of the air column becomes doubled
∴
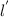 = 0.3 x 2
= 0.3 x 2
= 0.6 m
∴ New speed,
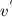 = 2 x 343
= 2 x 343
= 686 m/s
∴ New frequency is
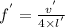

= 283 Hz
∴ The new frequency remains the same.
Now we know
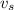 = 12 m/s,
= 12 m/s,
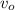 = 4 m/s,
= 4 m/s,
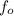 = 1975 Hz
= 1975 Hz
Therefore, apparent frequency is
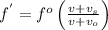

= 2020.5 Hz