Question

Write an equation of the line through(2-1) and perpendicular to 2yx-4 Write the equation in the form x The one the Enter your answer in the box and then click Check Answer parts showing i Type here to search

Answer 1

`2x+y=3`

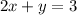
Explanation:

Here we aer given a point (2,-1) and a line
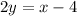`2y=x-4`. We are supposed to find the equation of the line passing through this point and perpendicular to this line.

Let us find the slope of the line perpendicular to
`2y=x-4`

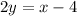
Dividing above equation by 2 we get

`y=(1)/(2)x-2`

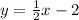
Hence we have this equation in slope intercept form and comparing it with

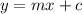`y=mx+c` , we get Slope
`m = (1)/(2)`

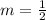
We know that product of slopes of two perpendicular lines in -1

Hence if slope of line perpendicular to
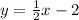`y=(1)/(2)x-2` is m' then

`m* m' =-1`

`(1)/(2) * m' =-1`

`m'=-2`

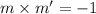
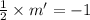
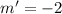
Hence the slope of the line we have to find is -2

now we have slope and a point

Hence the equation of the line will be

`(y-(-1))/(x-2)=-2`

`y+1=-2(x-2)`

`y+1=-2x+4`

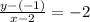
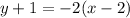
adding 2x and subtracting on both sides we get

`2x+y=3`

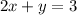
Which is our equation asked