Question

Use the disk method to find the volume of the solid generated when the region bounded by y equals 11 sine x and y equals 0​, for 0 less than or equals x less than or equals pi​, is revolved about the​ x-axis. (recall that sine squared x equals one half left parenthesis 1 minus cosine 2 x right parenthesis ​.)

Answer 1

(121/2)π² ≈ 597.111 cubic units

Explanation:

The volume is the integral of a differential of volume over a suitable domain. The problem statement tells us that the differential of volume should be a disk, so we have ...

dV = A·dx = πy²·dx = π·(11sin(x))²dx = 121π/2(1 -cos(2x))dx

Then the integral is ...

`\displaystyle V=\int_(0)^(\pi)(121\pi)/(2)(1-cos((2x)))\,dx=(121\pi)/(2)\left(\int_(0)^(\pi)1\,dx-\int_(0)^(\pi)cos((2x))\,dx\right)\\\\=(121\pi)/(2)(\pi -0)=(121\pi^2)/(2)`

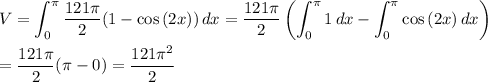
The volume of the solid is 60.5π² cubic units.