Question

Write a 6th order homogeneous linear equation whose general solution is

y=C1+C2e-t+C3Cos(3t)+C4sin(3t)+C5tcos(3t)+C6tsin(3t)

Answer 1

`y''''''+y'''''+18y''''+18y'''+81y''+81y'=0`

Explanation:

We are given that a general solution of 6th order homogeneous linear equation

`y=C_1+C_2e^(-t)+C_3 Cos(3t)+C_4 Sin(3t)+C_5 tCos(3t) +C_6 sin t (3t)`

We have to find the 6th order homogeneous linear differential equation whose general solution is given above.

We know that imaginary roots are in pair

There two values of imaginary roots and the values of imaginary roots are repeat.

From first term of general solution we get D=0

From second term of general solution we get D=-1

Last four terms are the values of imaginary roots and roots are repeated.

Therefore, D=
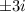`\pm 3i` and D=
`\pm 3i`

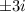
Substitute all values then we get

`D(D+1)(D^2+9)^2=0`

`D(D+1)(D^4+18D^2+81)=0`

`D^6+D^5+18D^4+18D^3+81 D^2+81 D=0`

`(D^6+D^5+18D^4+18D^3+81 D^2+81 D)y=0`

`y''''''+y'''''+18y''''+18y'''+81y''+81y'=0`

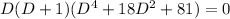
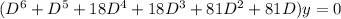
Therefore, the 6th order homogeneous linear differential equation is

`y''''''+y'''''+18y''''+18y'''+81y''+81y'=0`