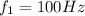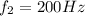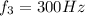Answer:
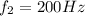
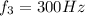
Step-by-step explanation:
Given:
Length of the string, L = 1 m
Mass per unit length, (m/L) = 2.0 × 10⁻³ kg/m
Tension in the string, T = 80N
Now, We know that,
Frequency,
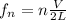 ................(1)
................(1)
where, V = velocity
also,
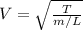
substituting the values in the equation we get
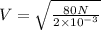
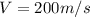
Now using the equation (1)
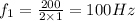
also,
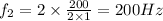
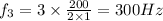
Hence, the required frequencies are