Question

(b) Released from rest at the same height, a can of frozen juice rolls to the bottom of the same hill. What is the translational speed of the frozen juice can when it reaches the bottom?

Answer 1

Step-by-step explanation:

a) using the energy conservation equation

mgh = 0.5mv^2 + 0.5Iω^2

I(moment of inertia) (basket ball) = (2/3)mr^2

mgh = 0.5mv^2 + 0.5( 2/3mr^2) ( v^2/r^2)

gh = 1/2v^2 + 1/3v^2

gh = v^2( 5/6)

v =
`\sqrt{(6gh)/(5) }`

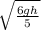
putting the values we get

`6.6 ^(2) = (6*9.8h)/(5)`

solving for h( height)

h = 3.704 m apprx

b) velocity of solid cylinder

mgh = 0.5mv^2 + 0.5( mr^2/2)( v^2/r^2) where ( I ofcylinder = mr^2/2)

g*h = 1/2v^2 + 1/4v^2

g*h = 3/4v^2

putting the value of h and g we get

v= = 6.957 m/s apprx