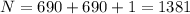Question

Two slits are separated by 0.380 mm. A beam of 550-nm light strikes the slits, producing an interference pattern. Determine the number of maxima observed in the angular range

Answer 1

total maximum on screen = 1381

Step-by-step explanation:

In the interference pattern we know that path difference for the position of maximum on the screen is given by

`\Delta L = d sin\theta`

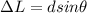
here we know that

`\theta` = angular position of maximum on screen

d = distance between two slits

`\Delta L = (0.380 mm)sin\theta`

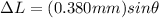
here we know that for all maximum positions

`\Delta L = N\lambda`

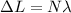
now plug in all values

`(0.380 * 10^(-3))sin\theta = N(550 * 10^(-9))`

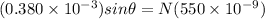
here we have

`sin\theta = 1.45 * 10^(-3)N`

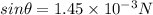
now we know that

`sin\theta < 1`

`1.45 * 10^(-3) N < 1`

`N < 690.9`

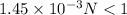
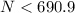
so total number of maximum on screen is

`N = 690 + 690 + 1 = 1381`