Question

The equation of motion of a particle is s = t3 − 3t, where s is in meters and t is in seconds. (Assume t ≥ 0.) (a) Find the velocity and acceleration as functions of t. g

Answer 1

Velocity:
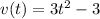`v(t) = 3t^(2) - 3` m/s

Accelaration:
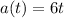`a(t) = 6t` m/s²

Step-by-step explanation:

The velocity is the derivative of the position.

The accelaration is the derivative of the velocity.

Derivative concepts

The derivative of
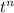`t^(n)` is
`n*t^(n-1)`

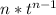
The derivative of a subtraction is the subtraction of the derivatives.

The derivative of a constant is 0.

The equation of the position is

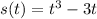`s(t) = t^(3) - 3t` m

The equation of the velocity is

Derivative of the position

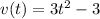`v(t) = 3t^(2) - 3` m/s

The equation of the acceleration is

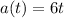`a(t) = 6t` m/s²

Answer 2

Step-by-step explanation:

The equation of motion of a particle is :

`s=t^3-3t`

Where

s is in meters

t is in seconds

The position of a particle is,
`v=(ds)/(dt)`

`v=(3t^2-3)\ m/s`

The acceleration of a particle is,
`a=(dv)/(dt)`

`a=(6t)\ m/s^2`

Hence, this is the required solution.