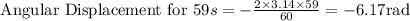Question

What is the angular displacement of the second hand on a clock after 59 seconds?

a.
-6.17 rad
c.
-2.01 rad
b.
-4.23 rad
d.
3.74 rad


Please select the best answer from the choices provided

A
B
C
D

thank you :)

Answer 1

a. -6.17 rad

Step-by-step explanation:

60 seconds is 2π radians. Writing a proportion:

2π / 60 = x / 59

x = 6.17

The displacement is negative because the second hand moves clockwise.

Answer 2

The angular displacement of the second hand on a clock after 59 second is -6.17 rad.

Answer: Option A

Explanation:

As we know angular displacement is defined as the change in the displacement in a circular motion for a given angle. So, angular displacement is derived using the formula

`\text { Angular Displacement }=\frac{\text { Total displacement }}{\text { Radius of the circular path }}`

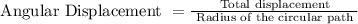
Also, in a clock the second hand travel a distance of 2π in 1 minute. If for 60 s, the angular displacement is 2π. Then for 1 s, the angular displacement will be

`\text { Angular Displacement for } 1 s=(2 \pi)/(60)`

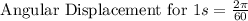
And for 59 seconds, the angular displacement will be

`\text { Angular Displacement for } 59 s=(2 \pi)/(60) * 59 \text { rad }`

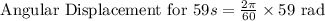
As we do not know the displacement of seconds hand after 59 seconds but the angular displacement will be having a negative sign as the clock hands move in clockwise direction. So ,

`\text { Angular Displacement for } 59 s=-(2 * 3.14 * 59)/(60)=-6.17 \mathrm{rad}`