Question

A wheel initially has an angular velocity of 18 rad/s, but it is slowing at a constant rate of 2 rad/s 2 . By the time it stops, it will have turned through approximately how many revolutions?

Answer 1

Answer:13 revolution

Explanation:

Given data

Wheel initial angular velocity
`\left ( \omega \right )`=18 rad/s

Contant angular deaaceleration
`\left ( \alpha \right )`=2
`rad/s^2`

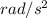
Time required to stop wheel completely=t sec

`\omega =\omega_0 + \aplha t`

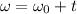
0 =18 +
`\left ( -2\right )t`

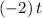
t=9 sec

Therefore angle turn in 9 sec

`\theta`=
`\omega_(0) t`+
`(1)/(2)`
`\left ( \alpha\right )t^(2)`

`\theta`=
`18* 9`+
`(1)/(2)`
`\left ( -2\right )\left ( 9\right )^2`

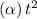
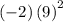
`\theta`=81rad

therefore no of turns(n) =
`(81)/(2* \pi)`

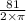
n=12.889
`\approx`13 revolution