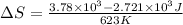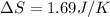Question

What is the total entropy change if a 0.280 efficiency engine takes 3.78E3 J of heat from a 3.50E2 degC reservoir and exhausts it to a 42.4 degC reservoir?

Answer 1

`\Delta S=1.69J/K`

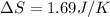
Step-by-step explanation:

We know,

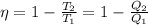`\eta=1-(T_2)/(T_1)=1-(Q_2)/(Q_1)` ..............(1)

where,

η = Efficiency of the engine

T₁ = Initial Temperature

T₂ = Final Temperature

Q₁ = Heat available initially

Q₂ = Heat after reaching the temperature T₂

Given:

η =0.280

T₁ = 3.50×10² °C = 350°C = 350+273 = 623K

Q₁ = 3.78 × 10³ J

Substituting the values in the equation (1) we get

`0.28=1-(Q_2)/(3.78* 10^(3))`

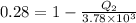
or

`(Q_2)/(3.78* 10^3)=0.72`

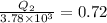
or

`Q_2=3.78* 10^3*0.72`

⇒
`Q_2 =2.721* 10^3 J`

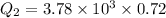
Now,

The entropy change (
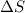`\Delta S`) is given as:

`\Delta S=(\Delta Q)/(T_1)`

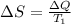
or

`\Delta S=(Q_1-Q_2)/(T_1)`

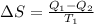
substituting the values in the above equation we get

`\Delta S=(3.78* 10^(3)-2.721* 10^3 J)/(623K)`

`\Delta S=1.69J/K`