Answer:
a)
 is an identity.
is an identity.
Explanation:
Most of the left hand sides are in this form:
 .
.
When you multiply conjugates you do not have to use full foil. You can just multiply the first and multiply the last or just use this as a formula:
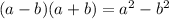 .
.
Choice a), b), and d). all have the form I mentioned.
So let's look at those choices for now.
a)
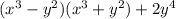
 (I used my formula I mentioned above.)
(I used my formula I mentioned above.)
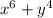
So this is an identity.
b)
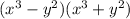
 (by use of my formula above)
(by use of my formula above)
This is not the right hand side so this equation in b is not an identity.
d)
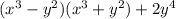

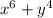
This is not the same thing as the right hand side so this equation in d is not an identity.
Let's look at c now.
c)
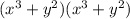
There is a formula for expanding this so that you could avoid foil. It is
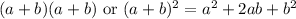 .
.
Just for fun I'm going to use foil though:
First: x^3(x^3)=x^6
Outer: x^3(y^2)=x^3y^2
Inner: y^2(x^3)=x^3y^2
Last: y^2(y^2)=y^4
---------------------------Add.

This is not the same thing as the right hand side.