Question

catering service offers 8 ​appetizers, 11 main​ courses, and 7 desserts. A banquet committee is to select 7 ​appetizers, 8 main​ courses, and 4 desserts. How many ways can this be​ done?

Answer 1

Answer: The required number of ways is 46200.

Step-by-step explanation: Given that a catering service offers 8 ​appetizers, 11 main​ courses, and 7 desserts.

A banquet committee is to select 7 ​appetizers, 8 main​ courses, and 4 desserts.

We are to find the number of ways in which this can be done.

We know that

From n different things, we can choose r things at a time in
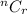`^nC_r` ways.

So,

the number of ways in which 7 appetizers can be chosen from 8 appetizers is

`n_1=^8C_7=(8!)/(7!(8-7)!)=(8*7!)/(7!*1)=8,`

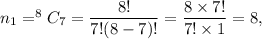
the number of ways in which 8 main courses can be chosen from 11 main courses is

`n_2=^(11)C_8=(11!)/(8!(11-8)!)=(11*10*9*8!)/(8!*3*2*1)=165`

and the number of ways in which 4 desserts can be chosen from 7 desserts is

`n_3=^7C_4=(7!)/(4!(7-4)!)=(7*6*5*4!)/(4!*3*2*1)=35.`

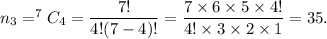
Therefore, the number of ways in which the banquet committee is to select 7 ​appetizers, 8 main​ courses, and 4 desserts is given by

`n=n_1* n_2* n_3=8*165*35=46200.`

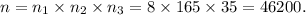
Thus, the required number of ways is 46200.