Final answer:
To produce an electric field of 1500 N/C just outside the surface of the plastic sphere, approximately 337.5 nC of excess charge must be distributed uniformly within its volume.
Step-by-step explanation:
To produce an electric field just outside the surface of the sphere, the excess charge on the surface of the sphere should be uniformly distributed within its volume. The electric field just outside a uniformly charged sphere is given by:
E = k * q / r2
Where E is the electric field, k is the Coulomb constant
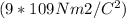 q is the charge, and r is the distance from the center of the sphere to the point outside the surface. In this case, E is given as 1500 N/C and r is half the diameter of the sphere (12.5 cm).
q is the charge, and r is the distance from the center of the sphere to the point outside the surface. In this case, E is given as 1500 N/C and r is half the diameter of the sphere (12.5 cm).
Substituting the values into the equation, we can solve for q:
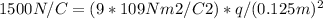
Solving for q, we find that the excess charge on the surface of the sphere should be approximately
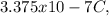 or about 337.5 nC.
or about 337.5 nC.