Answer:Expression given below
Step-by-step explanation:
Given mass of spring
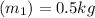
Compression in the spring
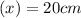
Let the spring constant be K
Using Energy conservation
potential energy stored in spring =Kinetic energy of Block
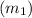
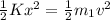
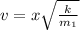
now conserving momentum
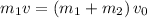
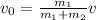
where
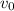 is the final velocity
is the final velocity